Hackear Protocolo Diffie-Hellman

El protocolo Diffie-Hellmanes un protocolo de establecimiento de claves entre partes que no han tenido contacto previo, utilizando un canal inseguro, y de manera anónima (no autentificada).

Su seguridad radica en la extrema dificultad (conjeturada, no demostrada) de calcular logaritmos discretos en un cuerpo finito.

Para demostrar como funciona, este protocolo maneja 2 valores por defecto:

• un número primo = p
• un generador del mismo numero primo = g

Ahora, suponiendo que dos personas "Alice" y "Bob" desean utilizar este protocolo para obtener una llave, necesitan saber cual es el número "p" y cual su generador "g".

Utilizando el protocolo y estableciendo los valores (sin alguna regla en especifico para seleccionar el numero "p") obtenemos que:

• p = 11
• g = 6 (Siendo "g" un generador de 11)

Ahora, Alice y Bob, respectivamente, seleccionarán un número al azar, el cual va a ser utilizado para generar su llave.

Suponiendo que Alice y Bob seleccionan números menores a "p" sin compartir el número entre ellos:

• a = 4
• b = 8

• Alice escoge  al azar, calcula , y envía  a Bob

     A = 6^4 mod 11

     A = 9

• Bob escoge 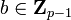 al azar, calcula , y envía  a Alice

    B = 6^8 mod 11

    B = 4

Para calcular sus llaves respectivamente, basta con que Alice comparta con Bob su valor "A" = 9 mientras que Bob comparte con Alice su valor "B" =4.

Nuevamente utilizando esos últimos valores "A" y "B" generamos una llave para cada Bob y Alice, que sera unica entre estos dos.

Alice calcula s = B^a mod p

• s = 4^4 mod 11
• s = 256 mod 11
• s = 3

Bob calcula s = A^b mod p

• s = 9^8 mod 11
• s = 43,046,721 mod 11
• s = 3

Hasta este punto tenemos "p", "g", "A","B" y "s" con lo cual podemos intentar un ataque de "fuerza bruta" recorriendo los posibles valores de "a" o "b" y así obtener la forma de descifrar la conversación entre Alice y Bob encontrando su llave "s".

Si sabemos que:

• p = 11
• g = 6
• A = 9
• B = 4

Entonces, necesitamos generar "n" números que sustituyan "a" y/o "b" y de esta forma podamos obtener "s" en las formulas:

• s = (g^a mod p = A)
• s = (g^b mod p = B)

Conclusiones:

Al tener que hacer un ataque de fuerza bruta para obtener la llave, es recomendable usar números grandes, principalmente en el numero primo "p", de tal forma que sea muy difícil quebrar nuestro protocolo.
Con esto tenemos un protocolo de conocimiento publico pero de una dificultad a tomar en cuenta y con un aceptable nivel de seguridad.